Question

Thirty percent of credit card holders carry no monthly balance, while 70% do. Of those card holders carrying a balance, 30% have annual income $20,000 or less, 40% between $20,001 - $50,000, and 30% over $50,000. Of those card holders carrying no balance, 20%, 30%, and 50% have annual incomes in these three respective categories.

a) What is the probability that a randomly chosen card holder has annual income $20,000 or less?
b) If this card holder has an annual income that is $20,000 or less, what is the probability that (s)he carries a balance?

Answer 1

a) 0.27 = 27% probability that a randomly chosen card holder has annual income $20,000 or less.

b) 0.778 = 77.8% probability that (s)he carries a balance

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

a) What is the probability that a randomly chosen card holder has annual income $20,000 or less?

20% of 30%(carry no balance).

30% of 70%(carry balance). So

`P = 0.2*0.3 + 0.3*0.7 = 0.06 + 0.21 = 0.27`

0.27 = 27% probability that a randomly chosen card holder has annual income $20,000 or less.

b) If this card holder has an annual income that is $20,000 or less, what is the probability that (s)he carries a balance?

Conditional probability.

Event A: Annual income of $20,000 or less.

Event B: Carries a balance.

0.27 = 27% probability that a randomly chosen card holder has annual income $20,000 or less

This means that
`P(A) = 0.27`

Probability of a income of $20,000 or less and balance.

30% of 70%, so:

`P(A \cap B) = 0.3*0.7 = 0.21`

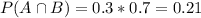
The probability is:

`P(B|A) = (P(A \cap B))/(P(A)) = (0.21)/(0.27) = 0.778`

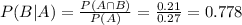
0.778 = 77.8% probability that (s)he carries a balance