Question

Study the function below and then answer the questions that follow. Equation What is the domain of f(x)? What is the range of f(x)?

Answer 1

Domain is

B)

(-infinity, -2) U (-2, infinity)

Range is (-4, infinity)

Explanation:

go it correct

edge2022

Answer 2

(a) Domain: All real numbers except -2

(b)
`f(x) > -4`

Explanation:

Given

See attachment for f(x)

Solving (a): The domain

From the attached image, we have:

`f(x) = -x - 2, x <-2`

`f(x) = -x^2, -2 < x < 0`

`f(x) = x, x \ge 0`

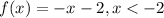
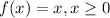
To get the domain, we consider the inequalities attached to each of the piece-wise function

`x < -2`

This implies that the values of x is less than -2 i.e.

`x = \{.......,-4,-3\}`

`-2< x<0`

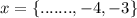
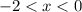
This implies that x is greater than -2 and less than 0 i.e.

`x = \{-1\}`

`x \ge 0`

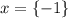
This implies that x is greater than or equal to 0 i.e.

`x =\{0,1,2,3,....\}`

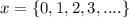
If these values of x are merged, we have:

`x = \{.......,-4,-3,-1,0,1,2,3.....\}`

`x = \{-\infty,..,-4,-3,-1,0,1,2,3,...,\infty\}`

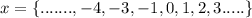
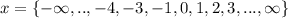
-2 is not included in the above values of x.

Solving (b): The range

From the attached image, we have:

`f(x) = -x - 2, x <-2`

`f(x) = -x^2, -2 < x < 0`

`f(x) = x, x \ge 0`

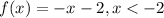
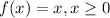
Substitute the greatest value of x in each piece-wise function.

`f(x) = -x - 2, x <-2`

`x=-2`

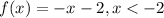
So;

`f(-2) = -2-2 = -4`

`f(x) = -x^2, -2 < x < 0`

`x = -2`

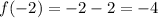
So:

`f(-2) = -2^2 = -4`

`f(x) = x, x \ge 0`

`x = \infty`

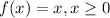
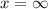
So;

`f(\infty) = \infty`

We have:

`f(-2) =-4`

`f(-2) =-4`

`f(\infty) = \infty`

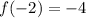
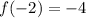
The smallest value of f(x) is -4

Hence, the range is:

`f(x) > -4`