Answer:
(c)
Explanation:
Given
See attachment for A and B
Required
Compare A and B
First, we get the initial population of A and B.
The initial population is at when
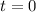
From the table of bacteria A, we have:
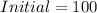 when
when
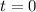
From the graph of bacteria B, we have:
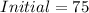 when
when
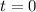
Since the initial of bacteria B is less than that of bacteria A, then (a) is incorrect.
Next, calculate the slope of A and B i.e. the rate
Slope (m) is calculated as:
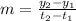
Where
y = Number of bacteria
t = time
For bacteria A:
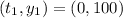
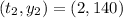
So, the slope is:
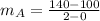
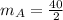
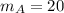
For bacteria B:
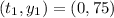
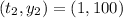
So, the slope is:
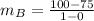
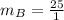
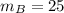
Since
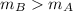 , then the rate of bacteria B is greater than that of bacteria A.
, then the rate of bacteria B is greater than that of bacteria A.
Hence, (d) cannot be true
Next, we determine the equation of both bacteria
This is calculated using:
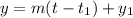
For bacteria A, we have:
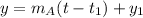
Where:
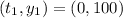
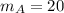
So:

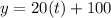
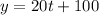
For bacteria B, we have:
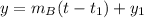
Where:
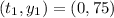
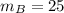
So:
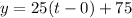
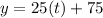
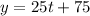
At 3 hours, the population of bacteria A is:
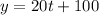
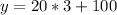
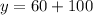
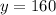
At 3 hours, the population of bacteria B is:
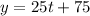
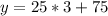
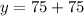
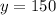
After 3 hours, bacteria B is 150 while A is 160.
This implies that (c) is correct because the population of B is less than that of A, at 3 hour
Lastly, to check if they will ever have equal population or not, we simply equate both equations.
So, we have:
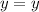

Collect like terms
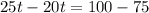
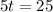
Solve for t
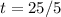
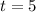
They will have equal population at 5 hours.
Hence, b is incorrect
From the above computation, only (c) is correct