Answer:
The rocket will hit the floor at 9.57 seconds
Explanation:
Given
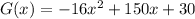
Take off height = 30ft
Initial velocity= 150ft/s
Required [Missing from the question]
Time to hit the ground
The rocket will hit the ground at:

So, we have:
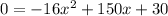
Rewrite as:
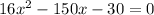
Solve using quadratic formula, we have:
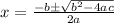
Where:
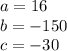
So, we have:
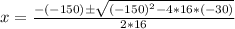
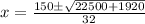


Split:

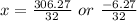
Time cannot be negative;
So:
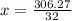

Hence, the rocket will hit the floor at 9.57 seconds