Given:
Either has a school certificate or diploma or even both = 20 people
Having school certificates = 14
Having diplomas = 11
To find:
The number of people who have a school certificate only.
Solution:
Let A be the set of people who have school certificates and B be the set of people who have diplomas.
According to the given information, we have
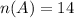
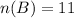
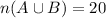
We know that,


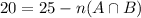
Subtract both sides by 25.


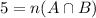
We need to find the number of people who have a school certificate only, i.e.
 .
.

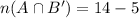

Therefore, 9 people have a school certificate only.