Slope-intercept form
Linear equations are often organized in slope-intercept form:

- (x,y) = a point that falls on the line
- m = the slope of the line
- b = the y-intercept of the line
Slope (m)
The slope of a line is equal to its
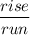 .
.
- "Rise" refers to the number of units the line travels up.
- "Run" refers to the number of units the line travels to the right.
Typically, we would solve for the slope by using the following formula:
 where two points that fall on the line are
where two points that fall on the line are
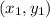 and
and
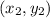
Y-intercept (b)
The y-intercept of a line refers to the y-value that occurs when x=0.
On a graph, it is the y-value where the line crosses the y-axis.
Writing the Equation
1) Determine the slope of the line (m)

Plug in the two given points, (-17,-4) and (-7,-13):
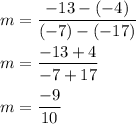
Therefore, the slope of the line is
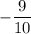 . Plug this into
. Plug this into
 :
:
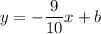
2) Determining the y-intercept (b)
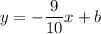
Plug in one of the given points and solve for b:
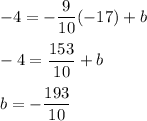
Therefore, the y-intercept of the line is
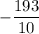 . Plug this back into our equation:
. Plug this back into our equation:

Answer
