Question

The velocity of a particle moving along a line is given by v(t) = e ^ t * sin(e ^ t) the interval 0<= t<= pi 2 . What is the distance that the particle traveled on this time interval?

Answer 1

0.44237 units

Explanation:

Given

`v(t) = e^t*sin(e^t)`

`0 \le t \le (\pi)/(2)`

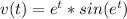
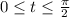
Required

The distance traveled in this interval

We have:

`v(t) = e^t*sin(e^t)`

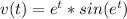
The distance is calculated as:

`d(t) = \int\limits^a_b {v(t)} \, dt`

So, we have:

`d(t) = \int\limits^{(\pi)/(2)}_0 {e^t*sin(e^t)} \, dt`

Let:

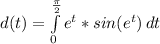
`u = e^t`

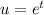
Differentiate

`(du)/(dt) = e^t`

So:

`dt = e^(-t) du`

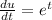
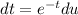
So, we have:

`d(t) = \int\limits^{(\pi)/(2)}_0 {e^t*sin(e^t)} \, dt`

`d(t) = \int\limits^{(\pi)/(2)}_0 {e^t*sin(u)} \, e^(-t) du`

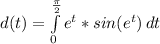
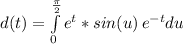
Rewrite as:

`d(t) = \int\limits^{(\pi)/(2)}_0 {e^t* e^(-t)*sin(u)} \, du`

`d(t) = \int\limits^{(\pi)/(2)}_0 {sin(u)} \, du`

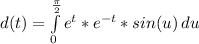
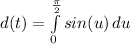
Integrate:

`d(t) = -\cos(u)|\limits^{(\pi)/(2)}_0`

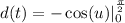
Substitute
`u = e^t`

`d(t) = -\cos(e^t)|\limits^{(\pi)/(2)}_0`

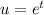
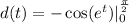
Split

`d(t) = -\cos(e^(\pi)/(2)) - [-\cos(e^0)]`

`d(t) = -\cos(e^(\pi)/(2)) +\cos(e^0)`

`d(t) = -0.09793 + 0.5403`

`d(t) = 0.44237`

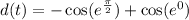
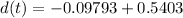
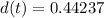
The distance traveled in this interval is: 0.44237 units

dt =

d(t) = \int\limits^2_0 {e^t*sin(e^t)} \, dt