Question

Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the x-axis. Verify your results using the integration capabilities of a graphing utility. y = e^(x-1), y=0, x=1, x=2

Answer 1

the volume of the solid generated by revolving the region bounded by the graphs of the equations about the x-axis is;

`(\pi )/(2) [e^2 - 1 ]` or 10.036

Explanation:

Given the data in the question;

y =
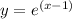`y = e^{(x - 1 )`, y = 0, x = 1, x = 2.

Now, using the integration capabilities of a graphing utility

y =
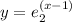`y = e_2}^{(x - 1 )_`, y = 0

Volume =
`\pi \int\limits^2_1 ( e^(x-1)^2) - (0)^2 dx`

Volume =
`\pi \int\limits^2_1 ( e^{x-1)^2 dx`

Volume =
`\pi \int\limits^2_1 e^(2x-2)dx`

Volume =
`(\pi )/(e^2) \int\limits^2_1 e^(2x)dx`

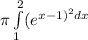
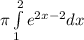
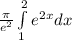
Volume =
`(\pi )/(e^2) [(e^(2x))/(2)]^2_1`

Volume =
`(\pi )/(2e^2) [e^4 - e^2 ]`

Volume =
`(\pi )/(2) [e^2 - 1 ]` or 10.036

Therefore, the volume of the solid generated by revolving the region bounded by the graphs of the equations about the x-axis is;

`(\pi )/(2) [e^2 - 1 ]` or 10.036