Question

In the figure the triangle is right triangle at *Y* and *N* is the foot of the perpendicular from *Y* to XZ. Given that XY=6 cm and XZ=10 cm. What is the length of XN

Answer 1

3.6cm

Explanation:

YZ = 10² - 6² = 8

sinX = 8/10 = 53.13º

cos 53.13º = XN/6

XN = 3.6cm

Answer 2

`\underline{ \underline{ \red{ \large {\tt{✧ G \: I \: V \: E \: N}}} }}:`

• XY = 6 cm , XZ = 10 cm

`\underline{ \underline{ \purple{ \large{ \tt{✧ T \: O \: \: F\: I\: N\: D}}}}} :`

• Length of XN

`\underline{ \underline{ \pink{\large {\tt{✧ S \: O \: L \: U\: T\: I \: O\: N}}}} }:`

• Let the length of XN be ' x ' & that of NZ be ' 10 - x '

In rt. XYZ :

• Hypotenuse (h ) = 10 , Perpendicular ( p ) = YZ & Base ( b ) = 6

Using Pythagoras theorem:

`\large{ \sf{p = \sqrt{ {h}^(2) - {b}^(2) } }}`

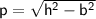
Plug the values & then simplify!

⇢
`\large{ \sf{YZ = \sqrt{( {10)}^(2) - {(6)}^(2) } }}`

⇢
`\large{ \sf{YZ = √(100 - 36)}}`

⇢
`\large{ \sf{YZ = √(64)}}`

⇢
`\large{ \sf{YZ = 8} \: cm} \:`

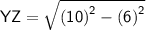
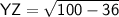
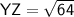
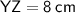
In rt. YNZ ,

• Hypotenuse = 8 cm , Perpendicular = YN , base = 10 - x

Using Pythagoras theorem :

⇾
`\large{ \sf{ {p}^(2) = {h}^(2) - {b}^(2) }}`

⇾
`\large{ \sf{ {YN}^(2) = {8}^(2) - {(10 - x)}}}^(2)`

⇾
`\large{ \sf{ {YN}^(2) = 64 - \{ {(10)}^(2) - 2 * 10 * x + {(x)}^(2) \} }}`

⇾
`\large{ \sf{ {YN}^(2) = 64 - \{100 - 20x + {x}^(2) \}}}`

⇾
`\large{ \sf{ {YN}^(2) = 64 - 100 + 20x - {x}^(2) }}`

⇾
`\large{ \sf{ {YN}^(2) = 20x - {x}^(2) - 36}} \longrightarrow \: eq (i)`

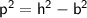
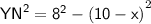
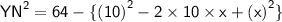
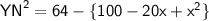
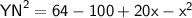
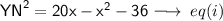
In rt. XYN ,

• Hypotenuse = 6 , Perpendicular = YN , base = x

Using Pythagoras theorem :

`\large{ \sf{ {p}^(2) = {h}^(2) - {b}^(2) }}`

⇾
`\large{ \sf{ {YN}^(2) = {(6)}^(2) - {(x)}}}^(2)`

⇾
`\large{ \sf{ {YN}^(2) = 36 - {x}^(2) \longrightarrow \: eq(ii) }}`

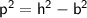
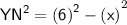
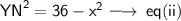
Now , From Equation ( i ) & Equation ( ii )

⤑
`\large{ \sf{20x - {x}^(2) - 36 = 36 - {x}^(2) }}`

⤑
`\large{ \sf{20x - \cancel{ {x}^(2) } - 36 = 36 - \cancel{ {x}^(2) }}}`

⤑
`\large{ \sf{20x = 36 + 36}}`

⤑
`\large{ \sf{20x = 72}}`

⤑
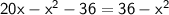
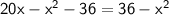
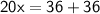
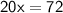
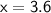`\large{ \sf{x = 3.6}}` cm

Hence, The length of XN is
`\large{ \boxed{\red{ \bold{ \tt{3.6 \: cm}}}}}`

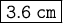
[ Correct me if I am wrong ]

♨ Hope I helped! ♡

♪ Have a wonderful day / night ! ☃

☥
`\underbrace{ \overbrace{{ \mathfrak{Carry \: On \: Learning}}}}` ✎

▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁