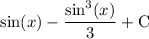Question

Help please!

integrate the following:

`\displaystyle \int \cos ^(3) (x) dx`
​

Answer 1

`\displaystyle \sin (x) - \frac{ { \sin}^(3) (x)}{3} + \rm C`

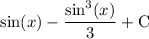
Explanation:

we would like to integrate the following integration

`\displaystyle \int \cos ^(3) (x) dx`

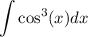
in order to do so rewrite

`\displaystyle \int \cos ^(2) (x) \cos(x) dx`

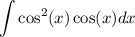
we can also rewrite cos²(x) by using trigonometric indentity

`\displaystyle \int( 1 - \sin ^(2) (x) )\cos(x) dx`

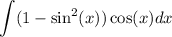
to apply u-substitution we'll choose

`\rm \displaystyle u = \sin ^{} (x) \quad \text{and} \quad du = \cos(x) dx`

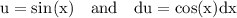
thus substitute:

`\displaystyle \int( 1 - {u}^(2) )du`

apply substraction integration and:

`\displaystyle \int 1du - \int {u}^(2) du`

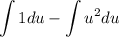
use constant integration rule:

`\displaystyle u - \int {u}^(2) du`

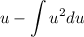
use exponent integration rule:

`\displaystyle u - \frac{ {u}^(3) }{3}`

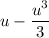
back-substitute:

`\displaystyle \sin (x) - \frac{ { \sin}^(3) (x)}{3}`

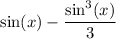
finally we of course have to add constant of integration:

`\displaystyle \sin (x) - \frac{ { \sin}^(3) (x)}{3} + \rm C`

Answer 2

i think its help..............