Question

A powerful women's group has claimed that men and women differ in attitudes about sexual discrimination. A group of 50 men (group 1) and 40 women (group 2) were asked if they thought sexual discrimination is a problem in the United States. Of those sampled, 11 of the men and 19 of the women did believe that sexual discrimination is a problem. Find the value of the test statistic. Round to two decimal places.

A. Z= - 1.20
B. Z= -2.55
C. Z= -1.05
D. Z= -0.85

Answer 1

B. Z= -2.55

Explanation:

To solve this question, first we need to understand the central limit theroem and subtraction of normal variables.

Central Limit Theorem

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

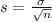For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
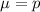`\mu = p` and standard deviation
`s = \sqrt{(p(1-p))/(n)}`

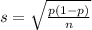
Subtraction of normal variables:

When two normal variables are subtracted, the mean is the subtraction of the means while the standard deviation is the square root of the sum of the variances.

11 of 50 men believe that sexual discrimination is a problem:

This means that:

`p_M = (11)/(50) = 0.22, s_M = \sqrt{(0.22*0.78)/(50)} = 0.0586`

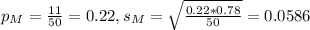
19 of 40 women believe that sexual discrimination is a problem:

This means what:

`p_W = (19)/(40) = 0.475,  s_W = \sqrt{(0.475*0.525)/(40)} = 0.079`

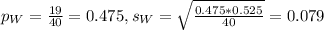
Difference between the proportion of men and women:

`p_D = p_M - p_W = 0.22 - 0.475 = -0.255`

`s_D = √(s_M^2+s_W^2) = √(0.0586^2+0.079^2) = 0.0984`

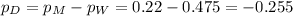
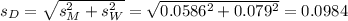
A powerful women's group has claimed that men and women differ in attitudes about sexual discrimination.

This means that the null hypothesis is that they do not differ, than is, the difference is 0. So

`H_0: p_D = 0`

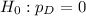
At the alternate hypothesis, we test that they differ, that is, the difference is different of 0. So

`H_a: p_D \\eq 0`

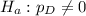
The test statistic is:

`z = (X - \mu)/(s)`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis and s is the standard error.

0 is tested at the null hypothesis:

This means that
`\mu = 0`

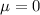
For the sample, we calculated that:

`X = -0.255, s = 0.0984`

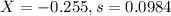
The value of the test-statistic is:

`z = (X - \mu)/(s)`

`z = (-0.255 - 0)/(0.0984)`

`z = -2.59`

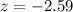
Closes answer is Z = -2.55, option B.