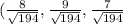Question

Essentials of University Mathematics

Example 3.
Find the length of the vector PQ from the point P(3.-5. 2) to the
point QC-5.4.9)
Find a unit vector with the direction of PQ

Answer 1

The length of the vector is of
`√(194)`

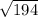
The unit vector with the direction of PQ is
`((8)/(√(194)), (9)/(√(194)), (7)/(√(194))`

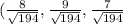
Explanation:

Vector from point P(3,-5,2) to Q(-5,4,9)

The vector is:

`PQ = Q - P = (-5-3, 4-(-5), 9-2) = (8,9,7)`

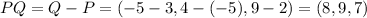
The length is:

`√(8^2+9^2+7^2) = √(194)`

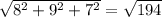
The length of the vector is of
`√(194)`

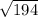
Find a unit vector with the direction of PQ

We divide each component of vector PQ by its length. So

`((8)/(√(194)), (9)/(√(194)), (7)/(√(194))`

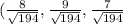
The unit vector with the direction of PQ is
`((8)/(√(194)), (9)/(√(194)), (7)/(√(194))`