Question

In figure 5.19 to the right PQRS is a rectangle. if PS=5cm and PR=13cm find SR and QS.​

Answer 1

Given:

PQRS is a rectangle.

`PS=5\ cm,\ PR=13\ cm`

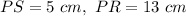
To find:

The length of SR and QS.

Solution:

We know that, all interior angles of a rectangle are right angle. So,
`\angle S=90^\circ`.

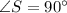According to the Pythagoras theorem, in a right angle triangle,

`Hypotenuse^2=Base^2+Perpendicular^2`

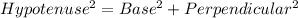
Using Pythagoras theorem in triangle PRS, we get

`PR^2=PS^2+SR^2`

`13^2=5^2+SR^2`

`169-25=SR^2`

`144=SR^2`

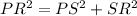
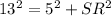
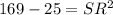
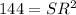
Taking square root on both sides.

`√(144)=SR`

`12=SR`

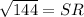
So, the measure of SR is 12 cm.

We know that the diagonals of a rectangle are equal. PR and QS are the diagonals of the rectangle PQRS. So,

`PR=QS`

`13=QS`

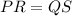
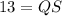
Therefore, the length of SR is 12 cm and the length of QS is 13 cm.