Answer:
Step-by-step explanation:
Here we'll use our formula for specific heat, Q=mcΔT.
Q= Heat (Joules), m=mass (g), c=specific heat
ΔT= (final temperature - initial temperature)
When we add a heated piece of metal in water at a lower temperature, the metal will lose heat and the water will absorb that heat. Over time they will eventually reach an equilibrium, here we have it at 21.9 C. If you recall in thermodynamics, , when we lose heat it is exothermic and the values of exothermic reactions are negative, and the values of endothermic reactions are positive. So we can say the heat of the metal is exothermic and releasing heat into the water until they reach equilibrium, thus they are equal. Keeping in mind Q= heat,
-Q metal = Q water.
We can expand this equation to -mcΔT= mcΔT.
Our equation reflects what is happening to the metal and the water.
Before we start, it might be helpful to remember that the
c=specific heat of water= 4.186 J/g C
Let's plug in what we know and solve for c=specific heat of metal. I'll start with the left side then go to the right side.
-(23.9g)(c)(29.9-97.8) = (52.4g)(4.184)(29.9 - 21.9)
-(23.9gc)(29.9-97.8) = (52.4g)(4.184)(29.9 - 21.9)
-(23.9g)(c)(-67.9) = (52.4g)(4.184)(29.9 - 21.9)
1623c = (52.4g)(4.184)(29.9 - 21.9)
1623c = (52.4g)(4.184)(8)
1623c = 1754
c=
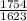
c= 1.08
This means it takes less heat to raise the temperature of the piece of metal ( in comparison to the water, which require more ).