1 Answer

Giovanny Gonzalez · Answer 1 · 2022-12-28T06:48:27+0000

Given:

The figure of circle E.
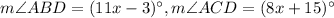$m\angle ABD=(11x-3)^\circ,m\angle ACD=(8x+15)^\circ$ .

To find:

The measure of arc AD.

Solution:

We know that the inscribed angles on the same arc are congruent and their measures are equal.

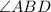$\angle ABD$ and
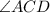$\angle ACD$ are inscribed angles on the same arc AD. So,

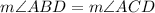
$m\angle ABD=m\angle ACD$

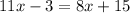
11x-3=8x+15

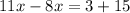
11x-8x=3+15

3x=18

x=6

Now,

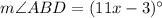
$m\angle ABD=(11x-3)^\circ$

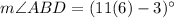
$m\angle ABD=(11(6)-3)^\circ$

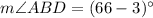
$m\angle ABD=(66-3)^\circ$

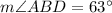
$m\angle ABD=63^\circ$

We know that the intercepted arc is always twice of the inscribed angle.

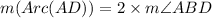
$m(Arc(AD))=2* m\angle ABD$

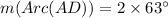
$m(Arc(AD))=2* 63^\circ$

$m(Arc(AD))=126^\circ$

Therefore, the measure of arc AD is 126 degrees.

Please log in or register to add a comment.