Question

3. What is the slope of the line that passes through points (-6, 1) and (4,-4)?

Answer 1

slope = (-4 - 1)/(4 - -6) = -5/10 = -1/2
Answer: -1/2

Answer 2

`\boxed {\boxed {\sf m= \frac {-1}{2}}}`

Explanation:

Slope is equal to the change in y over the change in x.

`m= \frac {y_2-y_1}{x_2-x_1}`

where (x₁, y₁) and (x₂, y₂) are the points the line passes through. We are given the points (-6, 1) and (4, -4). Therefore, if we match the values in the points to the corresponding variables:

• x₁= -6
• y₁= 1
• x₂= 4
• y₂= -4

Substitute the values into the formula.

`m= \frac {-4-1}{4--6}`

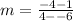
Solve the numerator.

• -4-1= -5

`m= \frac {-5}{4--6}`

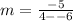
Solve the denominator.

• 4--6= 4+6=1-

`m= (-5)/(10)`

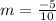
Simplify the fraction. Both the numerator and denominator are divisible by 5.

`m= \frac {-5/5}{10/5}`

`m= (-1)/(2)`

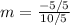
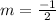
The slope of the line is -1/2