Question

Help Please!! Struggling with this for a while

Answer 1

Area of triangle ABC = 6 square units

Explanation:

By applying Pythagoras theorem in right triangle ADC,

AC² = AD² + CD²

3² = (1.8)² + CD²

9 - 3.24 = CD²

CD = √5.76

CD = 2.4 units

By applying mean ratio theorem,

`(AD)/(CD)=(CD)/(DB)`

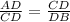
CD² = AD × DB

(2.4)² = 1.8 × DB

DB =
`(5.76)/(1.8)`

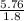
DB = 3.2 units

AB = AD + DB

AB = 1.8 + 3.2

AB = 5 units

Since, area of a triangle ABC =
`(1)/(2)(\text{Base})(\text{Height})`

=
`(1)/(2)(\text{AB})(\text{CD})`

=
`(1)/(2)(5)(2.4)`

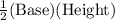
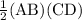
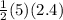
= 6 square units