Question

What is the mass in grams of 7.5 mol of C8H18?

Answer 1

`\boxed {\boxed {\sf 856.74 \ g \ C_8H _(18)}}`

Step-by-step explanation:

To convert from grams to moles, the molar mass is used. These values tells us the grams in 1 mole of a substance. They can be found on the Periodic Table (they are equivalent to the atomic masses, but the units are grams per mole).

We are given the compound C₈H₁₈. Look up the molar masses of the individual elements.

• Carbon (C): 12.011 g/mol
• Hydrogen (H): 1.008 g/mol

Notice there are subscripts that tell us the number of atoms of each element. We must multiply the molar masses by the subscripts.

• C₈: 8(12.011 g/mol)=96.088 g/mol
• H₁₈: 18(1.008 g/mol)=18.144 g/mol

Add these 2 values together to find the molar mass of the whole compound.

• C₈H₁₈: 96.088 g/mol +18.144 g/mol=114.232 g/mol

Use this number as a ratio.

`( 114.232 \ g \ C_8H_(18))/(1 \ mol \ C_8H_(18))`

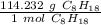
Multiply by the given number of moles: 7.5

`7.5 \ mol \ C_8H_(18)*( 114.232 \ g \ C_8H_(18))/(1 \ mol \ C_8H_(18))`

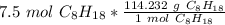
The moles of C₈H₁₈ will cancel each other out.

`7.5 *( 114.232 \ g \ C_8H_(18))/(1)`

`7.5 *{ 114.232 \ g \ C_8H_(18)}`

`856.74 \ g \ C_8H _(18)`

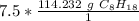
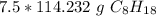
7.5 moles of C₈H₁₈ is equal to 856.74 grams of C₈H₁₈