Question

Model the Earth's atmosphere as 79% N2, 19% O2, and 2% Argon, all of which are in thermal equilibrium at 280 K. At what height is the density of O half its value at sea level

Answer 1

`9.495 * 10^3\ m`

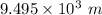
Step-by-step explanation:

From the given information:

Using the equation of Barometric formula as related to density, we have:

`\rho (z) = \rho (0) e^{(-(z)/(H))} \ \ \ \ --- (1)`

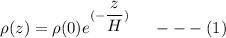
Here;

`p(z) =` the gas density at altitude z

`\rho(0) =` the gas density at sea level

H = height of the scale

`H = (RT)/(M_ag ) \ \ \ --- (2)`

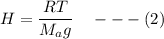
Also;

R represent the gas constant

temperature (T) a= 280 K

g = gravity

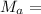`M_a =` molaar mass of gas; here, the gas is Oxygen:

∴

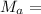`M_a =` 15.99 g/mol

= 15.99 × 10⁻³ kg/mol

`H = (8.3144 * 280)/(15.99 * 10^(-3) * 9.8 )`

`H =14856.43 \ m`

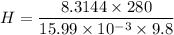
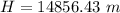
Now we need to figure out how far above sea level the density of oxygen drops to half of what it is at sea level.

This implies that we have to calculate z;

i.e.
`\rho(z) =(\rho(0) )/((2))`

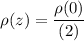
By using the value of H and
`\rho(z)` from (1), we have:

`(\rho(0) )/((2)) = \rho (0) e^{(-(z)/(14856.43))}`

∴

`(1)/(2) = e^{(-(z)/(14856.43))} \\ \\ e^{(-(z)/(14856.43))} =(1)/(2)`

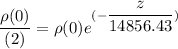
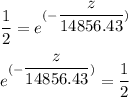
By rearrangement and taking the logarithm of the above equation; we have:

`- z = 14856.43 * \mathtt{In}(1)/(2) \\ \\ -z = 14856.43 * (-0.6391) \\ \\ z = 9495 \ m \\ \\ z = 9.495 * 10^3\ m`

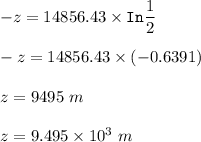
As a result, the oxygen density at
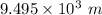`9.495 * 10^3\ m` is half of what it is at sea level.