Answer:
The value of the appropriate test statistic is Z = -2.71.
Explanation:
The mean annual starting salaries for college graduates with a degree in Operations Management was $65,000. We would like to determine whether or not this has decreased this year due to the pandemic.
This means that the null hypothesis is that the mean stays the same, that is:
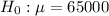
The alternative hypothesis is that it decreased, that is:

The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
65000 is tested at the null hypothesis:
This means that
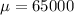
Data were collected over the annual starting salaries from a random sample of 40 Operations Management graduates. The average salary is $63,500 in the sample. Assume the standard deviation for the population of annual salaries is $3500.
This means that
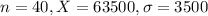
What is the value of the appropriate test statistic?



The value of the appropriate test statistic is Z = -2.71.