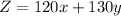Answer:
Max:
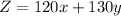
Subject to:
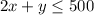
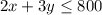
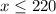
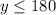
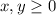
Step-by-step explanation:
Given
Let:
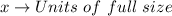
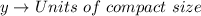
Required
Formulate a linear optimization model
Constraints for time:
For the general assembly (hours), we have the following parameters:

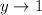
So, the expression is:
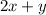 --- (1)
--- (1)
For the electronic assembly (hours), we have the following parameters:

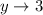
So, the expression is:
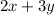 --- (2)
--- (2)
Solving further [Time available]:
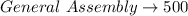
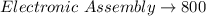
So, (1) and (2) becomes:
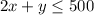
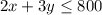
Constraints for selling:
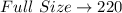 --- at most
--- at most
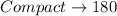 -- at most
-- at most
The above can be represented as:
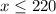
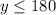
Earnings contribution:
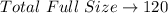
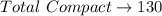
The objective function to be maximized can then be modelled as: