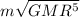Question

The motivation for Isaac Newton to discover his laws of motion was to explain the properties of planetary orbits that were observed by Tycho Brahe and analyzed by Johannes Kepler. A good starting point for understanding this (as well as the speed of the space shuttle and the height of geostationary satellites) is the simplest orbit--a circular one. This problem concerns the properties of circular orbits for a satellite orbiting a planet of mass M.

For all parts of this problem, where appropriate, use G for the universal gravitational constant.

Required:
a. Find the kinetic energy K of a satellite with mass m in a circular orbit with radius R.
b. Find the orbital period T.
c. Find L, the magnitude of the angular momentum of the satellite with respect to the center of the planet. Express your answer in terms of m, M, G, and R.

Answer 1

a) v² = G M R³, b) T = 2π /
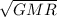`√(GMR)`, c)
`m √(GMR^5 )`

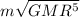
Step-by-step explanation:

a) The kinetic energy is

K = ½ m v²

to find the velocity let's use Newton's second law

F = m a

acceleration is centripetal

a = v² / R

force is the universal force of attraction

F = G m M / r²

we substitute

G m M R² = m v² R

v² = G M R³

the kinetic energy is

K = ½ m G M R³

b) angular and linear velocity are related

v = w R

w = v / R

w =
`(√(GMR^3 ))/(R)`

w =
`√(GMR)`

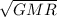
the angular velocity is related to the period

w = 2π / T

T = 2π / w

we substitute

T = 2π /
`√(GMR)`

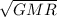
c) the angular moeomto is

L = m v r

L = m RA G M R³ R

L =
`m √(GMR^5 )`