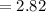Answer:
"2.82" seems to be the correct solution.
Explanation:
As we know,
A bag (Bag A) contains,
Red balls = 3
Blue ball = 1
A second bag (Bag B) contains,
Red balls = 1
Blue ball = 1
Now,
⇒ P(Bag A, red ball) =
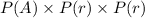
On substituting the values, we get
⇒ =
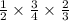
⇒ =

Similarly,
Probability of second bag will be:
⇒ P(Bag B) =

hence,
In the first bag (Bag A), the expected number of red balls will be:
⇒
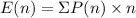
On substituting the values, we get
⇒
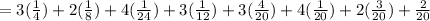
⇒
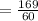
⇒