Question

A sample of 1300 computer chips revealed that 50% of the chips do not fail in the first 1000 hours of their use. The company's promotional literature states that 47% of the chips do not fail in the first 1000 hours of their use. The quality control manager wants to test the claim that the actual percentage that do not fail is different from the stated percentage. Make the decision to reject or fail to reject the null hypothesis at the 0.01 level.

Answer 1

The pvalue of the test is 0.03 > 0.01, which means that we fail to reject the null hypothesis at the 0.01 level.

Explanation:

The company's promotional literature states that 47% of the chips do not fail in the first 1000 hours of their use. The quality control manager wants to test the claim that the actual percentage that do not fail is different from the stated percentage.

This means that at the null hypothesis we test that the proportion is 47% = 0.47, that is:

`H_0: p = 0.47`

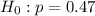
And at the alternate hypothesis, we test that the proportion is different from 47%, that is:

`H_a: p \\eq 0.47`

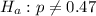
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

47% is tested at the null hypothesis:

This means that
`\mu = 0.47, \sigma = √(0.47*0.53)`

A sample of 1300 computer chips revealed that 50% of the chips do not fail in the first 1000 hours of their use.

This means that
`n = 1300, X = 0.5`

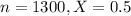
Value of the test statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (0.5 - 0.47)/((√(0.47*0.53))/(√(1300)))`

`z = 2.17`

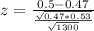
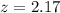
Pvalue of the test and decision:

The pvalue of the test is the probability that the proportion differs from 0.47 by at least 0.5 - 0.47 = 0.03, which is P(|Z| > 2.17), which is 2 multiplied by the pvalue of Z = -2.17

Z = -2.17 has a pvalue of 0.015

2*0.015 = 0.03

The pvalue of the test is 0.03 > 0.01, which means that we fail to reject the null hypothesis at the 0.01 level.