Answer:
sin(75°) =
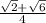
Explanation:
Given: sin(75°)
Rewrite: sin(30° + 45°)
Use sum and difference identity:
sin(α + β) = sinαcosβ + cosαsinβ
sin(30°+45°) = sin(30°)cos(45°) + cos(30°)sin(45°)
sin(30°+45°) = (1/2)(√2 / 2) + (√3 / 2)(√2 / 2)
sin(30°+45°) = (√2 / 4) + (√6 / 4)
sin(30°+45°) = [(√2 + √6) / 4]
sin(75°) = [(√2 + √6) / 4]