Question

A machine is shut down for repairs if a random sample of 100 items selected from the daily output of the machine reveals at least 15% defectives. (Assume that the daily output is a large number of items.) Suppose that a random sample of 20 items is selected from the machine. If the machine produces 20% defectives, find the probability that the sample will contain at least three defectives, by using the following methods. (a) the normal approximation to the binomial (Round your answer to four decimal places.)

Answer 1

0.7995 = 79.95% probability that the sample will contain at least three defectives.

Explanation:

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

Can be approximated to a normal distribution, using the expected value and the standard deviation.

The expected value of the binomial distribution is:

`E(X) = np`

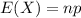
The standard deviation of the binomial distribution is:

`√(V(X)) = √(np(1-p))`

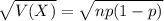
Normal probability distribution

Problems of normally distributed distributions can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

When we are approximating a binomial distribution to a normal one, we have that
`\mu = E(X)`,
`\sigma = √(V(X))`.

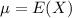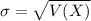Suppose that a random sample of 20 items is selected from the machine.

This means that
`n = 20`

The machine produces 20% defectives

This means that
`p = 0.2`

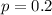
Mean and standard deviation:

`\mu = E(X) = np = 20*0.2 = 4`

`\sigma = √(V(X)) = √(np(1-p)) = √(20*0.2*0.8) = 1.79`

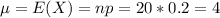
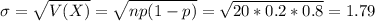
Probability that the sample will contain at least three defectives

Using continuity correction, this is
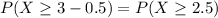`P(X \geq 3 - 0.5) = P(X \geq 2.5)`, which is 1 subtracted by the pvalue of Z when X = 2.5. So

`Z = (X - \mu)/(\sigma)`

`Z = (2.5 - 4)/(1.79)`

`Z = -0.84`

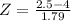
`Z = -0.84` has a pvalue of 0.2005

1 - 0.2005 = 0.7995

0.7995 = 79.95% probability that the sample will contain at least three defectives.