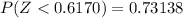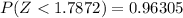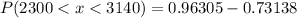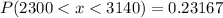Question

The average monthly mortgage payment for all homeowners in a city is $2870. Suppose that the distribution of monthly mortgages paid by homeowners in this city follow an approximate normal distribution with a mean of $2870 and a standard deviation of $470. Find to 4 decimal places the probability that the monthly mortgage paid by a randomly selected homeowner from this city is

Answer 1

The probability that the monthly mortgage is between 2300 and 3140 is: 0.23167

Explanation:

Given

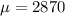`\mu = 2870` --- the average

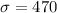`\sigma = 470` --- the standard deviation

Required [Missing from the question]

Monthly mortgage is between 2300 and 3140

This is represented as:

`P(2300 < x < 3140)`

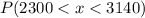
This is calculated as:

`P(a< x < b) = P(z_a < Z < z_b)`

`P(2300< x < 3140) = P(z_b < Z < z_a)`

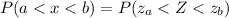
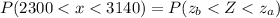
Calculate the z scores

`x = 3140`

`z = (3140 - 2850)/(470)`

`z = (290)/(470)`

`z = 0.6170`

`x = 2300`

`z = (3140 - 2300)/(470)`

`z = (840)/(470)`

`z = 1.7872`

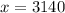
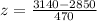
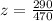
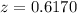
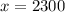
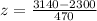
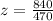
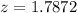
So, we have;

`P(2300< x < 3140) = P(1.1787 < Z < 0.6170)`

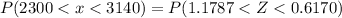
This is then calculated as:

`P(a < Z < b) = P(Z < a) - P(Z <b)`

`P(a < Z < b) = P(Z < 1.1782) - P(Z <0.6170)`

`P(2300< x < 3140) = P(Z < 1.1782) - P(Z <0.6170)`

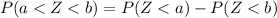
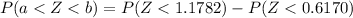
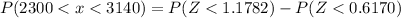
Using the z table:

`P(Z<0.6170) =0.73138`

`P(Z<1.7872) =0.96305`

`P(2300< x < 3140) = 0.96305 - 0.73138`

`P(2300< x < 3140) = 0.23167`