Question

11) A tank of kerosene with density of 750 kg/m3 has a syphon used to remove the fluid that then exits into the local atmosphere, with pressure of 101 kPa. The pressure above the kerosene in the tank is 120 kPa absolute. The syphon tube has a diameter of 2 cm, exits the tank rising to 10 cm above the level of the kerosene and then drops down to 15 cm below the level of the kerosene where it exits into the atmospheric pressure. Calculate the exit velocity from the tube.

Answer 1

`7.32\ \text{m/s}`

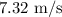
Step-by-step explanation:

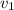`v_1` = Velocity at initial point = 0

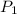`P_1` = Pressure in tank = 120 kPa

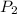`P_2` = Pressure at outlet = 101 kPa

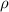`\rho` = Density of kerosene =
`750\ \text{kg/m}^3`

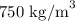
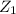`Z_1` = Tank height = 15 cm

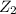`Z_2` = Height of pipe exit = 0

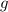`g` = Acceleration due to gravity =
`9.81\ \text{m/s}^2`

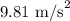
From Bernoulli's equation we have

`(P_1)/(\rho g)+(v_1^2)/(2g)+Z_1=(P_2)/(\rho g)+(v_2^2)/(2g)+Z_2\\\Rightarrow (P_1)/(\rho g)+Z_1=(P_2)/(\rho g)+(v_2^2)/(2g)\\\Rightarrow v_2=\sqrt{2g((P_1)/(\rho g)+Z_1-(P_2)/(\rho g))}\\\Rightarrow v_2=\sqrt{2* 9.81((120* 10^3)/(750* 9.81)+0.15-(101* 10^3)/(750* 9.81))}\\\Rightarrow v_2=7.32\ \text{m/s}`

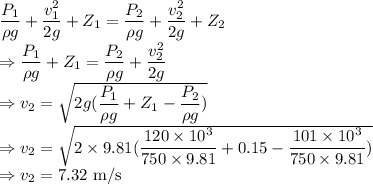
The exit velocity from the tube is
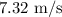`7.32\ \text{m/s}`.