Question

g A shopping center includes a grocery store and a drug store. One%E2%80%8B afternoon, a total of 200 people visited the shopping%E2%80%8B center, and 121 shopped at the grocery%E2%80%8B store, 91 shopped at the drug%E2%80%8B store, and 33 shopped at both businesses. %E2%80%8Ba) How many people shopped at the grocery store or the drug%E2%80%8B store? %E2%80%8Bb) How many people shopped at neither the grocery store nor the drug%E2%80%8B store?

Answer 1

a) 179 people shopped at the grocery store or the drug store.

b) 21 people shopped at neither the grocery store nor the drug store

Explanation:

I am going to treat these events as Venn sets.

I am going to say that:

Set A: Shopped at the grocery store

Set B: Shoped at the drug store.

121 shopped at the grocery store:

This means that
`A = 121`

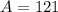
91 shopped at the drug store:

This means that
`B = 91`

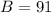
33 shopped at both businesses.

This means that
`A \cap B = 33`

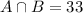
a) How many people shopped at the grocery store or the drug store?

This is

`A \cup B = A + B - (A \cap B)`

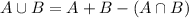
With the values given in the exercise.

`A \cup B = A + B - (A \cap B) = 121 + 91 - 33 = 179`

179 people shopped at the grocery store or the drug store.

b) How many people shopped at neither the grocery store nor the drug store?

179 of 200 shopped in at least one. So 200 - 179 = 21 shopped at neither.

21 people shopped at neither the grocery store nor the drug store