Question

A disk with mass 1.64 kg and radius 0.61 meters is spinning counter-clockwise with an angular velocity of 17.6 rad/s. A rod of mass 1.51 kg and length 1.79 meters spinning clockwise with an angular velocity of 5.12 rad/s is dropped on the spinning disk and stuck to it (the centers of the disk and the rod coincide). The combined system continues to spin with a common final angular velocity. Calculate the magnitude of the loss in rotational kinetic energy due to the collision

Answer 1

The loss in rotational kinetic energy due to the collision is 36.585 J.

Step-by-step explanation:

Given;

mass of the disk, m₁ = 1.64 kg

radius of the disk, r = 0. 61 m

angular velocity of the disk, ω₁ = 17.6 rad/s

mass of the rod, m₂ = 1.51 kg

length of the rod, L = 1.79 m

angular velocity of the rod, ω₂ = 5.12 rad/s (clock-wise)

let the counter-clockwise be the positive direction

let the clock-wise be the negative direction

The common final velocity of the two systems after the collision is calculated by applying principle of conservation of angular momentum ;

m₁ω₁ + m₂ω₂ = ωf(m₁ + m₂)

where;

ωf is the common final angular velocity

1.64 x 17.6 + 1.51(-5.12) = ωf(1.64 + 1.51)

21.1328 = ωf(3.15)

ωf = 21.1328 / 3.15

ωf = 6.709 rad/s

The moment of inertia of the disk is calculated as follows;

`I_(disk) = (1)/(2) mr^2\\\\I_(disk) = (1)/(2) (1.64)(0.61)^2\\\\I_(disk) = 0.305 \ kgm^2`

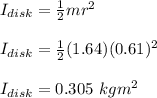
The moment of inertia of the rod about its center is calculated as follows;

`I_(rod) = (1)/(12) mL^2\\\\I_(rod) = (1)/(12) * 1.51 * 1.79^2\\\\I _(rod )= 0.4032\ kgm^2`

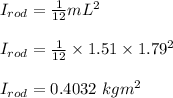
The initial rotational kinetic energy of the disk and rod;

`K.E_i = (1)/(2) I_(disk)\omega _1 ^2 \ \ + \ \ (1)/(2) I_(rod)\omega _2 ^2 \\\\K.E_i= (1)/(2) (0.305)(17.6) ^2 \ \ + \ \ (1)/(2) (0.4032)(-5.12) ^2\\\\K.E_i = 52.523 \ J`

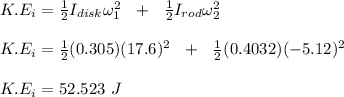
The final rotational kinetic energy of the disk-rod system is calculated as follows;

`K.E_f = (1)/(2) I_(disk)\omega _f ^2 \ \ + \ \ (1)/(2) I_(rod)\omega _f ^2\\\\K.E_f = (1)/(2) \omega _f ^2(I_(disk) + I_(rod))\\\\K.E_f = (1)/(2) (6.709) ^2(0.305+ 0.4032)\\\\K.E_f = 15.938 \ J`

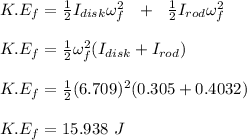
The loss in rotational kinetic energy due to the collision is calculated as follows;

`\Delta K.E = K.E_f \ - \ K.E_i\\\\\Delta K.E = 15.938 J \ - \ 52.523 J\\\\\Delta K.E = - 36.585 \ J`

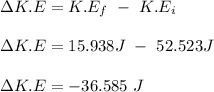
Therefore, the loss in rotational kinetic energy due to the collision is 36.585 J.