Answer:
8.5 ft (nearest tenth)
Explanation:
To find the depth of the pool at the deep end, we need to find the height of the right triangle with angle 16.5° and add it to 4.5 ft
Base of the triangle = 35 - 9 - 12.5 = 13.5 ft
Use the tan trig ratio:
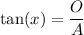
where x is the angle, O is the side opposite and angle and A is the side adjacent to the angle in a right triangle.
Given:
- x = 16.5°
- O = h (height)
- A = 13.5 ft
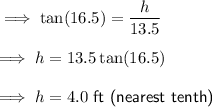
Therefore, the depth of the pool at the deepest end = 4 + 4.5 = 8.5 ft (nearest tenth)