Question

Question 1

10 pts
The vertices of a triangle are P(4,7), Q(-1,7) and R(4,-5). What is the
perimeter of triangle PQR?

Answer 1

30

Explanation:

This problem can be done without the Distance Formula (which is a way to find the distance between any two points in the plane).

The attached image shows the points and segments joining them.

PQ = 5 because the points are on the same horizontal line, and you can count spaces between them (or subtract x-coordinates: 4 - (-1) = 5).

PR = 12 because the points are on the same vertical line; count spaces or subtract y-coordinates, 7 - (-5) = 12.

The triangle is a right triangle, so the Pythagorean Theorem can be used to find the length of the hypotenuse.

`(\text{leg})^2+(\text{leg})^2=(\text{hypotenuse})^2`

`(QR)^2=5^2+12^2=25+144=169\\QR=√(169)=13`

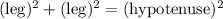
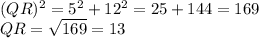
The perimeter of the triangle is 5 + 12 + 13 = 30