Question

A vehicle moves along a straight road. The vehicle's position is given by f(t) , where tt is measured in seconds since the vehicle starts moving. During the first 10 seconds of the motion, the vehicle's acceleration is proportional to the cube root of the time since the start. Which of the following differential equations describes this relationship, where k is a positive constant?

a. df/dt = kſ
b. df/dt - = kgf
c. d²f/dt = kyt dt2
d. d²f/dt = ky

Answer 1

The differential equation that describes this relationship, where k is a positive constant is option C.
`\( (d^2 f)/(dt^2) = k \sqrt[3]{t} \).`

How did we arrive at this assertion?

Let's analyze the given information and the differential equations.

The acceleration of the vehicle is proportional to the cube root of the time since the start. The acceleration is the second derivative of the position function with respect to time.

Let
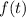`\( f(t) \)` be the position function. The acceleration
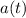`\( a(t) \)` is given by the second derivative
`\( a(t) = (d^2 f)/(dt^2) \).`

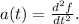
The given relationship is that
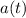`\( a(t) \)` is proportional to
`\( \sqrt[3]{t} \)`, where
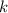`\( k \)` is a positive constant. Therefore, the correct differential equation is:

`\[ (d^2 f)/(dt^2) = k \sqrt[3]{t} \]`

So, comparing this with the given choices:

A.
`\( (d)/(dt)(f) = k \sqrt[3]{t} \)` - This is the first derivative of the position function, not the second derivative. Incorrect.

B.
`\( (d)/(dt)(f) = k \sqrt[3]{f} \)` - This is the first derivative of the position function, not the second derivative. Incorrect.

C.
`\( (d^2 f)/(dt^2 ) = k \sqrt[3]{t} \)` - This is the correct form for the differential equation. Correct.

D.
`\( (d^2 f)/(dt \cdot t^2) = k \sqrt[3]{f} \)` - This is not the correct form. Incorrect.

Therefore, the correct answer is C:
`\( (d^2 f)/(dt^2) = k \sqrt[3]{t} \).`

Correct question:

A vehicle moves along a straight road. The vehicle's position is given by f(t), where t is measured in seconds since the vehicle starts moving. During the first 10 seconds of the motion, the vehicle's acceleration is proportional to the cube root of the time since the start. Which of the following differential equations describes this relationship, where k is a positive constant?

A d/dt (f) = k * root(t, 3)

B d/dt (f) = k * root(f, 3)

C (d ^ 2 * f)/(d * t ^ 2) = k * root(t, 3)

D (d ^ 2 * f)/(d * t ^ 2) = k * root(f, 3)