Question

The surface area of a trianglular pyramid is 305 square inches. the area of the base is 35 square inches. Each face has a base of 9 inches. What is the slant height?

Answer 1

S=20 inches
Hope this helps

Answer 2

Slant height = 20 inches

Explanation:

To find the slant height of a triangular pyramid, we need to use the formula for the surface area of a triangular pyramid and then solve for the slant height.

The surface area (SA) of a triangular pyramid is given by:

`\boxed{\rm S.A. =\text{Area of the base}+ (1)/(2) \left(\text{Perimeter of the base} * \text{Slant height} \right)}`

In this case:

• S.A. = 305 in²
• Area of the base = 35 in²
• Perimeter of the base = 9 in + 9 in + 9 in = 27 in

Now, substitute these values into the surface area formula:

`305=35+(1)/(2)(27* \text{Slant height})`

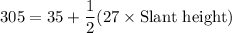
Now, solve for the slant height:

`270=(1)/(2)(27* \text{Slant height})`

`540=27* \text{Slant height}`

`\text{Slant height}=(540)/(27)`

`\text{Slant height}=20\; \rm inches`

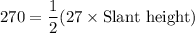
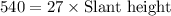
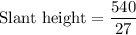
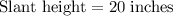
Therefore, the slant height of the triangular pyramid is 20 inches.