Question

A rectangular tent has a perimeter of 24 feet. Its area is 32 square feet. What are the dimensions of the tent?

Answer 1

4 feet by 8 feet

Step-by-step explanation:

Given

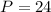`P =24` -- Perimeter

`A = 32` --- Area

Required

The dimension of the tent

The perimeter of a rectangle is:

`P =2(L + W)`

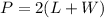
Where

`L = Length\\ W = Width`

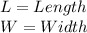
So, we have:

`2(L+W) = 24`

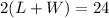
Divide both sides by 2

`L + W = 12`

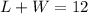
Make L the subject

`L = 12 - W`

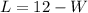
The area is calculated as:

`A = L* W`

This gives:

`L * W = 32`

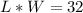
Substitute
`L = 12 - W`

`(12 - W) * W = 32\\`

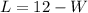
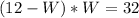
Open bracket

`12W - W^2 = 32`

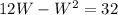
Express as quadratic equation

`W^2 - 12W - 32 = 0`

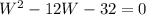
Expand

`W^2 - 8W -4W- 32 = 0`

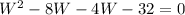
Factorize

`W(W - 8) -4(W- 8) = 0`

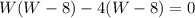
Factor out W - 8

`(W - 4)(W- 8) = 0`

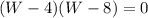
Split

`W - 4 = 0\ or\ W - 8 = 0`

Solve for W

`W =4\ or\ W = 8`

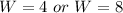
Recall that:

`L = 12 - W`

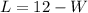
Substitute
`W =4\ or\ W = 8`

`L = 12 - 4 = 8`

`L = 12 - 8 = 4`

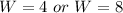
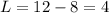
So, we have:

`W =4\ or\ W = 8`

`L = 8\ or\ L = 4`

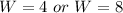
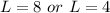
So, the dimension is: 4 feet by 8 feet