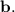The vector on the grid, from (2, 1) to (8, 5), is expressed as
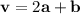 using vector decomposition with given vectors
using vector decomposition with given vectors
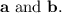
To express the vector drawn on the grid in terms of vectors
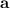 and
and
 , we can utilize the given vectors
, we can utilize the given vectors
 and
and
 . The vector on the grid starts from (2, 1) and ends at (8, 5). The displacement between these points represents the desired vector.
. The vector on the grid starts from (2, 1) and ends at (8, 5). The displacement between these points represents the desired vector.
The displacement vector
 can be obtained by subtracting the initial point from the terminal point:
can be obtained by subtracting the initial point from the terminal point:
![\[ \mathbf{v} = \begin{bmatrix} 8 - 2 \\ 5 - 1 \end{bmatrix} = \begin{bmatrix} 6 \\ 4 \end{bmatrix} \]](https://img.qammunity.org/2022/formulas/mathematics/college/ccmztvdv3azasmak6ulnyyiyr6ptuckeu1.png)
Now, to express
 in terms of
in terms of
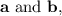 we can use vector decomposition. We want to find scalars
we can use vector decomposition. We want to find scalars
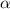 and
and
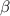 such that
such that

![\[ \begin{bmatrix} 6 \\ 4 \end{bmatrix} = \alpha \begin{bmatrix} 1 \\ 3 \end{bmatrix} + \beta \begin{bmatrix} 4 \\ -2 \end{bmatrix} \]](https://img.qammunity.org/2022/formulas/mathematics/college/c2qjysvg6chf2o2rjmf6ujwuzukjf3l4ca.png)
Solving for
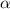 and
and
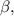 we find
we find
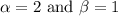 . Therefore, the vector
. Therefore, the vector
 can be expressed as:
can be expressed as:
![\[ \mathbf{v} = 2\mathbf{a} + \mathbf{b} \]](https://img.qammunity.org/2022/formulas/mathematics/college/bsl9jsr990qqnypur6u6khqsuybp5jxdjw.png)
In conclusion, the vector drawn on the grid can be expressed as twice vector
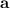 plus vector
plus vector