Answer:
B
Explanation:
we are given a equation of a line
we want to figure out the equation of the perpendicular line passes through the (6,5) points
in order to do so
recall that,
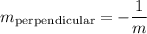
we got from our given equation that m=2
because equation of a line is y=mx+b
thus
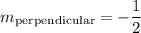
remember that, when we want to figure out perpendicular line or parallel line we should the formula given by
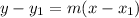
since we got our perpendicular m is -½,
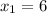 and
and
 , substitute
, substitute
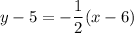
to get the perpendicular equation you should simplify the above equation to y=mx+b form
distribute -½:
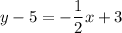
add 5 to both sides:
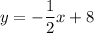
hence,
our answer choice is B