Answer:
The length of legs lm, mn, and lk is 32 while that of kn is 36.
Explanation:
The diagram is attached in the answer.
As both the angles are equal thus the two forms isosceles triangles. This is true because the converse of base angle theorem is applicable here. The theorem clearly states that when a trapezoid is divided by the diagonal, it forms two set of angles where m<1=m<2 and m<lmk=m<nmk
This leads the two set of legs such as

Or this could be written as
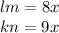
Now the remaining two sides are given as
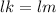 as this form an isosceles triangle so
as this form an isosceles triangle so
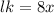
Similarly

Or

Now the perimeter is given as
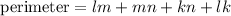
Here perimeter is given as 132 so this gives:
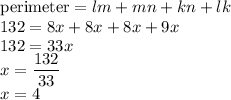
So the four legs are of length as given below:
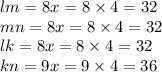
So the length of legs lm, mn, and lk is 32 while that of kn is 36.