Question

Given klmn is a trapezoid, kl = mn, m<1 = m<2, lm/kn = 8/9, pklmn = 132. Find: the length of the legs

Answer 1

The length of legs lm, mn, and lk is 32 while that of kn is 36.

Explanation:

The diagram is attached in the answer.

As both the angles are equal thus the two forms isosceles triangles. This is true because the converse of base angle theorem is applicable here. The theorem clearly states that when a trapezoid is divided by the diagonal, it forms two set of angles where m<1=m<2 and m<lmk=m<nmk

This leads the two set of legs such as

`(lm)/(kn)=(8)/(9)`

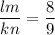
Or this could be written as

`lm=8x\\kn=9x`

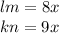
Now the remaining two sides are given as

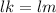`lk=lm` as this form an isosceles triangle so

`lk=8x`

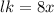
Similarly

`mn=lm\\`

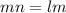
Or

`mn=8x`

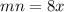
Now the perimeter is given as

`\text{perimeter}=lm+mn+kn+lk\\`

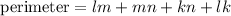
Here perimeter is given as 132 so this gives:

`\text{perimeter}=lm+mn+kn+lk\\132=8x+8x+8x+9x\\132=33x\\x=(132)/(33)\\x=4`

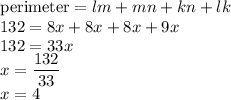
So the four legs are of length as given below:

`lm=8x=8* 4=32\\mn=8x=8* 4=32\\lk=8x=8* 4=32\\kn=9x=9*4=36`

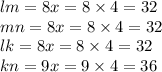
So the length of legs lm, mn, and lk is 32 while that of kn is 36.