Question

A baby's crib has an area of 690:square inches and a perimeter of 106 inches.What are the dimensions of the crib

Answer 1

The crib is 30 inches wide and 23 inches long.

Explanation:

Assuming that the crib is rectangular, then the crib has a length L and a width W.

And remember that for a rectangle of width W and length L, the perimeter is:

P = 2*L + 2*W = 2*(L + W)

And the area is:

A = L*W

In this case, the perimeter is 106 in, then:

P = 106in = 2*(L + W)

And we also know that the area is 690 in^2

Then:

A = 690in^2 = L*W

Then we have a system of equations:

106in = 2*(L + W)

690in^2 = L*W

To solve this, first, we need to isolate one of the variables in one of the equations.

Let's isolate L in the first one:

106in/2 = L + W

53 in = L + W

53in - W = L

Now we can replace this in the other equation:

690in^2 = L*W = (53in - W)*W = 53in*W - W^2

690in^2 = 53in*W - W^2

Now we need to solve this for W.

This is a quadratic equation:

W^2 - 53in*W + 690 in^2 = 0

The solutions of this equation are given by Bhaskara's formula:

`W = (-(-53in)\pm √((-53in)^2 - 4*1*(690in^2)) )/(2) = (57in \pm 7in)/(2)`

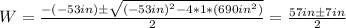
Then the two possible solutions of W are:

W = (53in + 7in)/2 = 30in

W = (53in - 7in)/2 = 23in

We can choose any one of these, so let's choose W = 30in

If we replace this in the equation: "53in - W = L"

We can find the value of L:

53in - 30in = 23in = L

Then we have:

W = 30in

L = 23in