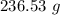Question

If 186.0 liters of gaseous O_{2} at 1.09 atm and 577.0 ºC are required for the model rocket to climb 1000 feet, how many grams of solid KClO_{3} must be in the rocket engine?

Answer 1

The right answer is "236.53 g".

Step-by-step explanation:

The given values are:

P = 1.09 atm

V = 186 liters

The reaction will be:

⇒
`KClO_3 (s)\rightarrow 2Kcl(s)+3O_2(g)`

The moles of O₂ will be:

=
`(PV)/(RT)`

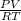
On substituting the values, we get

=
`(1.09* 186)/(0.0821* 850)`

=
`(202.47)/(69.785)`

=
`2.90 \ moles`

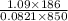
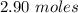
Now,

1 mole O₂ is produced from

=
`(2)/(3) \ mol \ KClO_3`

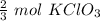
then,

2.90 mole O₂ is produced from 2 mol KClO₃

=
`(2)/(3)* 2.90`

=
`1.93 \ mol \ KClO_3`

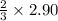
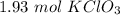
hence,

The number of grans of solid in the engine will be:

=
`1.93* 122.55`

=
`236.53 \ g`