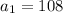Question

Find
`a_(1)` in a geometric series for which
`S_(n)` = 189, r =
`(1)/(2)`, and
`a_(n)` = 3.

Answer 1

`\displaystyle a_(1) = 108`

Explanation:

we are given

the sum,common difference and nth term of a geometric sequence

we want to figure out the first term

recall geometric sequence

`\displaystyle S_{ \text{n}} = \frac{ a_(1)(1 - {r}^(n) )}{1 - r}`

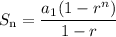
we are given that

• 
  `S_n=189`
• 
  `r=(1)/(2)`
• 
  `n=3`

thus substitute:

`\displaystyle 189= \frac{ a_(1)(1 - {( (1)/(2) )}^(3) )}{1 - (1)/(2) }`

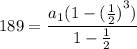
to figure out
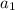`a_1` we need to figure out the equation

simplify denominator:

`\displaystyle \frac{ a_(1)(1 - {( (1)/(2) )}^(3) )}{ (1)/(2) } = 189`

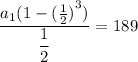
simplify square:

`\displaystyle \frac{ a_(1)(1 - {( (1)/(8) )}^{} )}{ (1)/(2) } = 189`

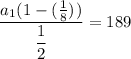
simplify substraction:

`\displaystyle ( a_(1) ((7)/(8) ))/( (1)/(2) ) = 189`

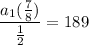
simplify complex fraction:

`\displaystyle a_(1) ((7)/(8) ) / { (1)/(2) } = 189`

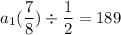
calculate reciprocal:

`\displaystyle a_(1) (7)/(8) * 2 = 189`

reduce fraction:

`\displaystyle a_(1) (7)/(4) \ = 189`

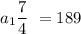
multiply both sides by 4/7:

`\displaystyle a_(1) (7)/(4) * (4)/(7) \ = 189 * (4)/(7)`

reduce fraction:

`\displaystyle a_(1) = 27* 4`

simplify multiplication:

`\displaystyle a_(1) = 108`

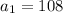
hence,

`\displaystyle a_(1) = 108`