The gradiant y=2x³-5x+1 at point (2,7)

Question

asked Nov 28, 2022 107k views

1 Answer

Sam Bisbee · Answer 1 · 2022-12-03T22:17:31+0000

Given:

The equation of the curve is:

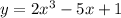
y=2x^3-5x+1

To find:

The gradient (slope) of the given curve at point (2,7).

Solution:

We have,

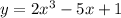
y=2x^3-5x+1

Differentiate the given equation with respect to x.

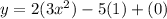
y=2(3x^2)-5(1)+(0)

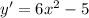
y'=6x^2-5

Now we need to find the value of this derivative at (2,7).

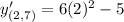
y'_((2,7))=6(2)^2-5

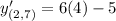
y'_((2,7))=6(4)-5

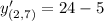
y'_((2,7))=24-5

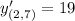
y'_((2,7))=19

Therefore, the gradient (slope) of the given curve at point (2,7) is 19.