Question

Unit 11: Value & Surface Area

Homework 1: Area of planes Figure
Pls Help me with #11

Answer 1

The area of the triangle is 351cm^2.

Explanation:

To find the area of a triangle, the formula is (1/2) x base x height. In this case, the height would be a line that cuts straight through the center of the triangle. However, this height is not given to us. We can still find it through Pythagoras' Theorem though.

Let A be the tip of the triangle, and B and C be the points on either side of the triangle. Assuming an imaginary line that cuts the triangle in a symmetrical half, let T be the point at the end of the line, directly below point A.

Using Pythagoras' Theorem,

AB^2 = AT^2 + TB^2

AT^2 = AB^2 - TB^2

AT^2 = 30^2 - (26/2)^2

AT^2 = 30^2 - 13^2

AT =

`\sqrt{ {30}^(2) - {13}^(2) }`

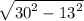
AT = 27.0370116692

So the length of AT is our height. We can now find the area of the triangle.

Area of triangle = (1/2) x 26cm x AT

Area of triangle = 351.4811516996

Area of triangle = 351cm^2 (To 3s.f.)