Answer:
a. 304 feet
b. 425 feet
c. 3.75 seconds
d. It will take the rocket approximately 8.9 seconds to hit the ground
Explanation:
1. The given data of the question including the question relationships are listed as follows;
The height of the cliff from which the rocket was launched = 200-ft.
The initial velocity of the rocket, u = 120 feet per second
The equation that models the height of the rocket with respect to time 't' is h(t) = -16·t² + 120·t + 200
a. The height of the rocket after 1 second is given by plugging in t = 1 in the equation that models the height as follows;
h(1) = -16 × (1)² + 120 × (1) + 200 = 304
The height of the rocket after 1 second, h(1) = 304 feet
b. The maximum height can be found by finding the value of the maximum point of the curve of the equation for the height as follows;
At the maximum point, h'(t) = d(-16·t² + 120·t + 200)/dt = 0
∴ d(-16·t² + 120·t + 200)/dt = -32·t + 120 = 0
t = 120/32 = 3.75
At the maximum point, t = 3.75 seconds
The maximum height can also be found by finding the vertex of the parabola formed by the height equation as follows;
At the vertex (the maximum point), t = -b/(2·a) = -120/(2 × (-16)) = 3.75
At the vertex (the maximum point), t = 3.75
The height at the maximum point = h(3.75) = -16 × (3.75)² + 120 × (3.75) + 200 = 425
The height at the maximum point, h(3.75) = 425 feet
c. The time it will take the rocket to reach the maximum point is given by the value of 't' at the maximum point, the vertex, which is t = -b/(2·a) = -120/(2 × (-16)) = 3.75
Therefore;
The time it takes the rocket to reach the maximum point,
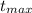 = 3.75 seconds
= 3.75 seconds
d. The time it takes the rocket to hit the ground (height h(t)) is given by finding the values of 't' that satisfy the height equation where h(t) = 0 as follows;
At the ground level, h(t) = 0 = -16·t² + 120·t + 200
Therefore, we get;
-16·t² + 120·t + 200 =
t = (-120 ± √(120² - 4×(-16) × 200))/(2 × (-16))
t ≈ 8.9 or t ≈ -1.4
Therefore, the time it takes the rocket to hit the ground is given by the natural number, t ≈ 8.9 seconds.