Given:
Base of the larger figure = 30 yd
Base of the smaller figure = 12 yd
To find:
a) The ratio of the perimeters of the larger figure to the smaller figure.
b) the ratio of the area of the larger figure to the smaller figure.
Solution:
a) We know that, the ratio of perimeters pf similar figures is equal to the ratio of their sides.
The given figures are similar. So, the ratio of the perimeters is:
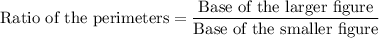
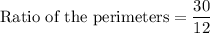
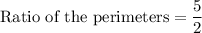
b) The ratio of area of similar figures is equal to the ratio of squares of their sides.
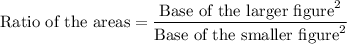
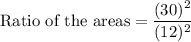
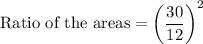
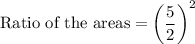
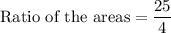
Therefore, the correct option is A.