Answer:
You could make 4,641,000 different choices.
Explanation:
The order in which the cards are chosen is not important, which means that the combinations formula is used to solve this question.
Combinations formula:
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

How many different choices could I make?
3 cards from a set of 52(number of cards on a standard deck).
4 Pokemon cards from a set of 10. So
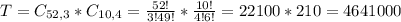
You could make 4,641,000 different choices.