Answer:
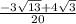
This is the single fraction of -3*sqrt(13)+4*sqrt(3) up top all over 20.
sqrt = square root
=======================================================
Step-by-step explanation:
Angle theta is between pi and 3pi/2. This places the angle in quadrant Q3 where both cosine and sine are negative
Use the pythagorean trig identity to get the following:
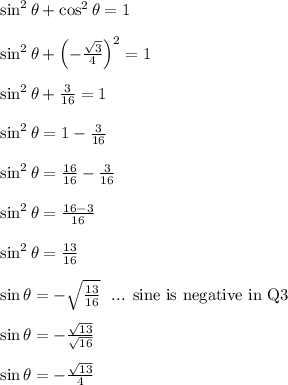
Angle beta is in Q1 where sine and cosine are positive.
Draw a right triangle with legs 3 and 4. The hypotenuse is 5 through the pythagorean theorem. In other words, we have a 3-4-5 right triangle.
Since
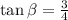 , this means
, this means
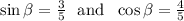
Use these ideas:
- sin = opposite/hypotenuse
- cos = adjacent/hypotenuse
- tan = opposite/adjacent
In this case we have: opposite = 3, adjacent = 4, hypotenuse = 5.
-------------------------------------
To recap:

They lead to this
