Question

The midpoint of the segment as an ordered pair (-6,-1,) (-1,-6)

Answer 1

`\boxed{\sf{(-3.5 , -3.5)}}}`

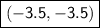
Explanation:

This problem must be solved using the midpoint formula, which is similar to a slope formula.

Midpoint formula:
`\sf{(X_1,Y_1)}(X_2,Y_2)`

`\sf{((x_2+x_1)/(2),\quad (y_2+y_1)/(2))}`

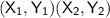
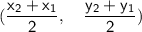
y2=(-6)

y1=(-1)

x2=(-1)

x1=(-6)

Rewrite the problem and then solve it.

`\left((-1-6)/(2),\:(-6-1)/(2)\right)=-\sf{(7)/(2), -(7)/(2)}`

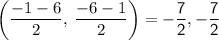
Dividing is another option.

-7/2=-3.5

(-3.5, -3.5)

As a result, the final answer is (-3.5, -3.5).

I hope this helps! Let me know if my answer is wrong or not.

Answer 2

Explanation:

(-6,-1) & (-1,-6)

`Midpoint=\left((x_(1)+x_(2))/(2),(y_(1)+y_(2))/(2) \right)\\\\\\=\left((-6-1)/(2),(-1-6)/(2) \right)\\\\\\=\left((-7)/(2),(-7)/(2) \right)\\\\\\`

= (-3.5 , -3.5)