Question

. Government Waste In a Gallup poll 513 national adults aged 18 years or older who consider themselves to be Republican were asked, "Of every tax dollar that goes to the federal government in Washington, D.C., how many cents of each dollar would you say are wasted?" The mean wasted was found to be 54 cents with a standard deviation of 2.9 cents. The same question was asked of 513 national adults aged 18 years or older who consider themselves to be Democrat. The mean wasted was found to be 41 cents with a standard deviation of 2.6 cents. Construct a 95% confidence interval for the mean difference in government waste, mR - mD. Interpret the interval.

Answer 1

Part A

The 95% confidence interval is approximately 12.66 ≤
`m_R` -
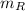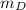`m_D` ≤ 13.34

Part B

We are 95% confident that the true difference in the mean amount of waste per dollar stated by the two categories of adults is larger than zero and it is approximately between 12.66 and 13.34

Explanation:

Part A

The given parameters are;

The mean amount adults that consider themselves Republican say is wasted for every dollar,
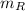`m_R` = 54 cents

The standard deviation of the statistics, s₁ = 2.9 cents

The number of respondents in the group, n₁ = 513

The mean amount adults that consider themselves Democrats say is wasted for every dollar,
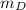`m_D` = 41 cents

The standard deviation of the statistics, s₂ = 2.6 cents

The number of respondents in the group, n₂ = 513

The F-test, F = s₁²/s₂² = 2.9²/2.6² = 1.244

The critical-t, t* = 1.962

F ≤ t*, therefore, we pool the data

`s_p =\sqrt{(\left ( n_(1)-1 \right )\cdot s_(1)^(2) +\left ( n_(2)-1 \right )\cdot s_(2)^(2))/(n_(1)+n_(2)-2)}`

`s_p =\sqrt{(\left ( 513-1 \right )\cdot 2.9^(2) +\left ( 513-1 \right )\cdot 2.6^(2))/(513+513-2)} = √(7.585)`

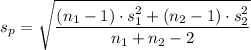
The 95% confidence interval is given by the following formula;

`\left (m_R- m_D \right )\pm t^* \cdot s_p \cdot\sqrt{(1)/(n_(1))+(1)/(n_(2))}`

The test statistic, is given as follows;

`t = \frac{m_R - m_D}{s_p *\sqrt{ (1)/(n_1) + (1)/(n_2)} }`

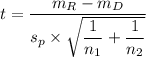
Therefore;

`t = \frac{54 - 41}{√(7.585) *\sqrt{ (1)/(513) + (1)/(513)} } \approx 75.598`

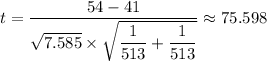
Given that the test statistic, t = 75.598 > The critical-t, t* = 1.962, we reject the null hypothesis, therefore, there is significant statistical evidence to suggest that there is a difference in the mean stated by the two sets

`s_p =\sqrt{(\left ( 513-1 \right )\cdot 2.9^(2) +\left ( 513-1 \right )\cdot 2.6^(2))/(513+513-2)} = √(7.585)`

`C. I. = \left (54- 41 \right )\pm 1.962 * √(7.585) * \sqrt{(1)/(513)+(1)/(513)}`

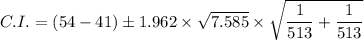
The 95% confidence interval, C.I. ≈ 12.66 ≤
`m_R` -
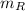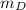`m_D` ≤ 13.34

Part B

From the 95% confidence interval, we are 95% confident that the true difference in the mean amount adult who consider themselves Republicans say politicians waste and the true difference in the mean amount adult who consider themselves Democrats say politicians waste is between 12.66 and 13.34

Given that there is no '0' in the range of values in the 95% confidence for the difference in mean from the two groups, difference in the mean amount of waste per dollar observed by the two categories of adults.